Θα έχετε όλοι παρατηρήσει πως, όταν κοιτάμε από κάπου ψηλά (π.χ. από ένα βουνό) βλέπουμε και πιο μακριά στον ορίζοντα.
Παρακάτω θα σας υποδείξω έναν τρόπο να υπολογίζετε πόσο μακριά μπορείτε να δείτε στον ορίζοντα, ανάλογα με το ύψομετρο πάνω από τη θάλασσα όπου βρίσκεστε.
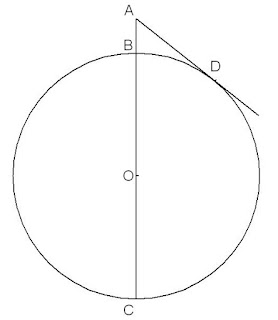
Σε ένα θεώρημα της ευκλείδιας γεωμετρίας της Β' Λυκείου αποδεικνυόταν το παρακάτω (βλέπετε και Σχήμα):
(ΑΒ) x (AC) = (AD)2 (1)
όπου
(BC): η διάμετρος του κύκλου (περνάει από το κέντρο Ο του κύκλου),
Α: σημείο πάνω από τον κύκλο που αποτελεί προέκταση της ευθεία BC και
(AD) η εφαπτομένη του κύκλου στο σημείο D που περνάει από το σημείο Α.
Τώρα η σειρά σας... θεωρείστε ότι παρατηρείτε τον ορίζοντα από το σημείο Α πάνω από τη Γή. Η όραση μας (αν υποθέσουμε ότι δεν υπάρχουν εμπόδια όπως σκόνη, ομίχλη, λόφοι, κλπ) φτάνει μέχρι το σημείο D του ορίζοντα.
Σημείωση: κανονικά η απόσταση που βλέπουμε μακριά στον ορίζοντα αντιστοιχεί στο τόξο ΒD και όχι η ευθεία ΑD. Ωστόσο, το μεγαλύτερο υψόμετρο που μπορεί να βρεθούμε στη βιόσφαιρα της Γης είναι μικρότερο από 10 km. Σε σύγκριση με την ακτίνα της Γης (6370 km) αυτό το υψόμετρο είναι κάτι πολύ μικρό. Έτσι πρακτικά το τόξο ΒD είναι ίσο με την ευθεία ΑD.
Παράδειγμα 1:
(ΑΒ)=10 μέτρα (υψόμετρο)
Ξέρουμε ότι (ΑC)=(AB)*(BC)=(10m)+(2*6370*10^3m)
Επομένως από (1) προκύπτει ότι: (ΑD)= 11287 m ή 11,3km
Παράδειγμα 2:
(ΑΒ)= 100 μέτρα (υψόμετρο)
Ξέρουμε ότι (ΑC)=(AB)+(BC)=(100m)+(2*6370*10^3m)
Επομένως από (1) προκύπτει ότι: (ΑD)= 35693 m ή 35,7km
Παράδειγμα 3:
(ΑΒ)= 2 μέτρα (υψόμετρο)
Ξέρουμε ότι (ΑC)=(AB)+(BC)=(2m)+(2*6370*10^3m)
Επομένως από (1) προκύπτει ότι: (ΑD)= 5048 m ή 5,0km
Παράδειγμα 4:
(ΑΒ)= 500 μέτρα (υψόμετρο)
Ξέρουμε ότι (ΑC)=(AB)+(BC)=(500m)+(2*6370*10^3m)
Επομένως από (1) προκύπτει ότι: (ΑD)= 79814 m ή 79,8km