Several
types of sundials exist. In this article guidance is given in order
to make two types of sundials:
- Equatorial sundial, and
- Analemmatic sundial.
There
is also a manual written about how to use the sundials and read the
time properly.
The
figures you are going to see apply for places in the Northern
Hemisphere of the Earth. However, directions will be given in order
to apply also for places in the Southern Hemisphere.
Let’s
begin…:
EQUATORIAL SUNDIAL
Advantages:
An equatorial sundial is easy to design and construct. It can work in
most places of the Earth.
Disadvantages:
There are corrections that need to be made when we read the time.
Furthermore, at latitudes (φ)
between 0<φ<23.5ο
north or south of the equator the equatorial sundial will
not show the correct time
(unless you could tilt the frame of the hours at the right angle
-facing south or north- depending on the place and the season-date).
Below
there are some figures for making an equatorial sundial for places in
the northern hemisphere.
Below there is a picture of an equatorial sundial that I made (in Greece):
At the picture above you may notice that the 13 hour is in the middle, instead of the 12 hour. I did this on purpose because the sundial is used more often during the summer season, where summer time is on. That is why I replaced the hours according to summer time so that I do not have to make corrections from standard time (winter time) to summer time.
Orientation
of the sundial
The
sundial must be placed horizontally, looking to the true
north-south direction as shown in the figures above.
The
magnetic north is not in the same direction as the true north
(geographic north).
By
the time the sun gets to its highest point in the sky (at solar
noon), turn the sundial so that the gnomon’s shadow shows 12 on the
sundial. This is one way to orientate your sundial towards the true
north-south direction.
But
how to find which time (of our watches) the sun is at solar noon? You
can find it in the internet, or you can contact with me.
User
Manual for an equatorial sundial
Since
you have orientated the sundial you should not move it again.
The
hours that you read on the sundial are according to standard time
(winter time). When
the Daylight Saving Time (DST or summer time) exists,
you should add 1
hour.
Example:
The gnomon’s shadow shows 11 o’clock and summer time exists. Then
we should make this correction (add 1 hour) and say that it is 12
o’clock.
Furthermore,
the orbit of the Earth around the sun is not an absolute circle (it
is called elliptic). That causes Earth to rotate around it’s axis a
little slower or a little faster, depending how close is Earth to the
sun. That means there will be differences between the time our
sundial shows and the time our watches show. That’s why we should
make the following corrections (shown in Table
1):
Table
1. Corrections
regarding the frequency of a complete rotation of the Earth around
its axis.
From Jan 1st
till Jan 15th
: Subtract 5 minutes of an hour (- 00:05)
|
From Jan
16th
till Jan 31st
: Subtract 10 minutes of an hour (- 00:10)
|
From Feb 1st
till Feb 28th
: Subtract 10 minutes of an hour (- 00:10)
|
From Mar 1st
till Mar 15th
: Subtract 10 minutes of an hour (- 00:10)
|
From Mar 16th
till Mar 31st
: Subtract 5 minutes of an hour (- 00:05)
|
From Apr 1st
till Apr 15th
: Do not make any correction
|
From Apr 16th
till Apr 30th
: Add 5 minutes of an hour (+ 00:05)
|
From May 1st
till May 31st
: Add 5 minutes of an hour (+ 00:05)
|
From Jun 1st
till Jun 15th
: Add 5 minutes of an hour (+ 00:05)
|
From
Jun 16th
till Jun 30th
: Do not make any correction
|
From
Jul 1st
till Jul 31st
: Do not make any correction
|
From
Aug 1st
till Aug 31st
: Do not make any correction
|
From Sep 1st
till Sep 15th
: Add 5 minutes of an hour (+ 00:05)
|
From Sep 16th
till Sep 30th
: Add 10 minutes of an hour (+ 00:10)
|
From Oct 1st
till Oct 15th
: Add 15 minutes of an hour (+ 00:15)
|
From Oct 16th
till Oct 31st
: Add 20 minutes of an hour (+ 00:20)
|
From Nov 1st
till Nov 15th
: Add 20 minutes of an hour (+ 00:20)
|
From Nov 16th
till Nov 30th
: Add 15 minutes of an hour (+ 00:15)
|
From Dec 1st
till Dec 15th
: Add 10 minutes of an hour (+ 00:10)
|
From
Dec 16th
till Dec 31st
: Do not make any correction
|
Finally,
corrections have to be made because the solar
noon is not reached
in every place on Earth always at 12 o’clock (local time). This is
due to the Longitude of the place in relation with the Time Zone it
belongs. Corrections should also include this factor. In Table
2 there is an
example of such corrections needed for Greece and Cyprus. For any
other place, there are differences. I can send you the corresponding
corrections for any place of the Earth. I just need to know the
Longitude and the Time Zone of the place.
Table
2. Corrections
based on the Longitude and the Time Zone for Greece and Cyprus.
Longitude (degrees)
|
Time Zone
|
Correction: add(+) /
subtract (-)
|
GREECE
|
GMT+02:00
|
|
19
o East
|
+ 44 minutes
|
|
20
o East
|
+ 40 minutes
|
|
21
o East
|
+ 36 minutes
|
|
22
o East
|
+ 32 minutes
|
|
23
o East
|
+ 28 minutes
|
|
24
o East
|
+ 24 minutes
|
|
25
o East
|
+ 20 minutes
|
|
26
o East
|
+ 16 minutes
|
|
27
o East
|
+ 12 minutes
|
|
28
o East
|
+ 8 minutes
|
|
29
o East
|
+ 4 minutes
|
|
CYPRUS
|
GMT+02:00
|
|
32
o East
|
- 8 minutes
|
|
33
o East
|
-12 minutes
|
|
34
o East
|
-16 minutes
|
|
35
o East
|
-20 minutes
|
EXAMPLE
1:
An
equatorial sundial has been placed in Thessaloniki (Greece) which has
Longitude 23o
East. The date is June 1st
(summer time). The sundial shows 11:30. The corrections that must be
made will be:
- Because we have summer time we add 1 hour (+01:00).
- From Table 1 we add 5 minutes (+00:05).
- From Table 2 we add 28 minutes (+00:28).
Therefore,
the time is finally 11:30 + 01:00 + 00:05 + 00:28 = 13:03
according to our watches.
EXAMPLE
2:
An
equatorial sundial has been placed in Heraklion (Greece) which has
Longitude 25o
East. The date is February 1st
(winter time). The sundial shows 11:30. The corrections that must be
made will be:
- Because we have winter time we make no correction.
- From Table 1 we subtract 10 minutes (-00:10).
- From Table 2 we add 20 minutes (+00:20).
Therefore,
the time is finally 11:30 + 00:00 - 00:10 + 00:20 = 11:40
according to our watches.
ANALEMMATIC SUNDIAL
This
type of sundial can also be used as a compass! Furthermore, (almost)
no corrections are needed when reading the time of the sundial’s
hour frame. However, the gnomon should be moved on its proper
position according to the date.
Below
there is a figure and a photograph of an analemmatic sundial –
compass:
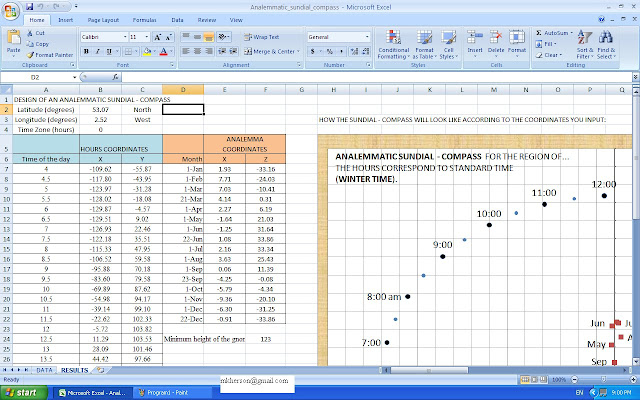
The
design of an analemmatic sundial is more complex compared to the
equatorial sundial. The calculation of the coordinates of the hours
and of the analemma (the one with “8” shape where dates are
written) takes longer time. Nevertheless, I made an effort and succeeded an automatic procedure. In an Excel file I wrote the formulas of
calculations and results derive automatically. One should just input
the data needed, such as the Geographic Coordinates and the Time Zone
of the place where the sundial is going to be set.
See
the following images of this Excel program:
Note:
The coordinates of the hours and of the analemma have resulted
randomly. That means that you can adjust these values to whichever
size (dimension) you want.
If
you are interested, I will be happy to send you the coordinates of
the hours and of the analemma so that you make your own sundial -
compass.