The radiation energy budgets are referred to:
a) the inflow of solar radiation (insolation) towards the Earth's atmosphere and surface,
b) the outflow of the Earth's (infrared/ longwave) radiation from the top of the atmosphere to the space and
c) transmission (scattering, convection, diffusion, reflection, evaporation), absorption or re-emission of radiation energy (solar or Earth's) among the surface of the Earth, the atmosphere and the top of the atmosphere.
I had seen that there where radiation energy budgets for the whole planet (e.g. from NASA). However there where very few radiation energy budgets for certain places, at least in a simple image/ figure. Furthermore I couldn't find simplified information about the seasonal variance in radiation energy budgets. It is very important to know the seasonal fluctuations if we want to have a better understanding of a region's climate. The annual average values could be deceiving. For instance, in Larissa (Greece) the average annual temperature is 15,8 oC, but through the winter season and the summer season the mean temperature is 6,2 oC and 26,3 oC correspondingly. Furthermore we have daily fluctuations of the climatic characteristics (weather) which are also very important for the understanding of the climate.
I had the idea to make a figure of the radiation energy budget for the region of the Aegean Sea, like the figure NASA gives for the whole planet (http://science-edu.larc.nasa.gov/energy_budget/pdf/ERB-poster-combined-update-3.2014.pdf). Thus, I managed to make figures of radiation energy budget for the Aegean Sea in an annual base, but also for every season (winter, spring, summer, autumn). I do not know how reliable and scientifically correct is this effort but, for me, regardless all that, it was a chance to learn (and to discover) some things.
In every figure that I submit there is a summary of the most important information that I think someone can export by studying it.
In the end of this work, I present the sources (bibliography) which I used.
There is also an annex where I explain the methodology I used to make all these radiation energy budgets.
The Earth's radiation energy budget
When scientists make an annual radiation energy budget for the whole planet we observe that it is zero or close to zero. This means that the inflows of solar energy that comes through the atmosphere is equal (or almost equal) with the outflow of the Earth's (infrared) radiation out to the space. If the annual energy budget remained positive or negative for a series of decades, then that could mean that probably the Earth's equilibrium is moving to warmer or colder time periods.
At Figure 1 the Earth's annual radiation energy budget given from NASA is presented. The values of the energy flows are written in Watt/m2 (W/m2).
Figure 1. Radiation energy budget of the Earth. It refers to annual mean values of energy fluxes in Watt/m2. Source:(http://science-edu.larc.nasa.gov/energy_budget/pdf/ERB-poster-combined-update-3.2014.pdf).
Before the reader proceeds, it would be useful to visit the website above in order to learn how these energy flows where estimated. Thus he/she will learn for example that the Earth's mean annual temperature is 15 oC or 288,15 oK (degrees Kelvin). He/she will learn about the “atmospheric window” and about the atmosphere's ability to trap heat and work as a blanket that holds the Earth's radiation preventing the surface from extreme temperatures.
Also, from the energy budget NASA has published, the reader will observe that there is zero balance (or almost zero balance) over three levels:
a) at the top of the atmosphere:
340,4 – 77 – 22,9 – 239,9 ≈ 0
b) in the atmosphere:
77,1 + 358,2 + 18,4 + 86,4 – 340,3 – 29,9 – 269,9 ≈ 0
c) at the surface of the Earth:
163,3 + 340,3 – 398,2 – 18,4 – 86,4 ≈ 0
Note: Infrared radiation of Earth (398,2) ≈ Absorption from the atmosphere (358,2) + Atmospheric window (40,1)
The “atmospheric window” is the Earth's (infrared - warm) radiation flow (of specific wavelength range) - emitted by the Earth's surface - that escapes directly to the outer space, without being absorbed from the ingredients of the atmosphere. The major components of the atmosphere that hold (absorb) radiation energy of the so called atmospheric window are the clouds (water vapor) and carbon dioxide (CO2).
The Earth as a whole is presented as a system with zero or almost zero balance of energy flows (on an annual base). That does not necessary mean individual parts of the Earth have also zero balance of energy budget. On the contrary, there are places with positive energy balance (excess of solar radiation that reaches the surface) and places with negative energy balance (deficit of solar radiation that reaches the surface). For instance, the polar regions have negative energy balance, while the tropical/subtropical regions have positive energy balance. Generally, regions in latitudes smaller than 38o (degrees) have surplus in their energy budget, while places in latitudes bigger than 38o have deficiency in their energy budget. All these budgets are considered in an annual base. However, there might be a season (e.g. summer or winter) where the energy balance is different from the annual budget.
The above differences in energy budgets (not only in space but also in time) are the cause of the various weather patterns on Earth (winds, ocean currents, rains, evaporation, etc.). Thus, through these meteorological conditions the energy is redistributed, from warmer to colder regions of the Earth.
Radiation energy budgets for the Aegean Sea
Below, figures of energy budgets are presented for the region of the Aegean Sea. Effort has been made so that budgets are created on an annual base and also for each season (winter, spring, summer, autumn).
I tried to make these figures like the one of Figure 1, which comes from NASA's publications.
The Aegean Sea was considered as a united sea (without land), although the meteorological data such as air temperature where gathered from stations of four islands: Crete, Rhodes, Naxos and Lesvos.
In Figure 2 the average annual energy budget of the Aegean Sea is presented.
Figure 2. Energy budget for the Aegean Sea on an average annual base. The values of energy fluxes are written in W/m2.
Top of the atmosphere: 343,8 – 79,7 – 259 = 5,1 W/m2.
In the atmosphere: 71,1 + 345,7 + (-2,7) + 117,3 – 332,4 – 18,8 – 175,2 = 5,0 W/m2.
At the surface (sea): 192,9 + 332,4 – 410,7 – (-2,7) – 117,3 = 0 W/m2.
It seems that over the Aegean Sea there is a slightly positive energy budget on an annual base. That is, the solar radiation energy that enters the atmosphere until the surface (sea) is a little larger than the emitted Earth's radiation energy that escapes to the space by 5,1 W/m2.
At the surface (sea) the energy budget is zero. This is a result of the methodology used for estimating the energy flows. It also results from the thought that the sea is being warmed over some months and is being cooled for the rest months of the year, so that in an annual base, there is a zero balance in sea temperature – energy budget of the surface. Evidently there must be sea currents that carry heat energy but there were not considered at the calculations. I think that these fluxes from sea currents should be small and neutral on an annual time period.
The negative sensible heat (-2,7 W/m2) for me means that the sea is marginally warmed from the atmosphere (winds) on an average annual time period.
In Figure 3 the energy budget of the Aegean during the winter season is presented.
Figure 3. Energy budget of the Aegean Sea during the winter season. Values of energy fluxes are written in W/m2.
Top of the atmosphere: 210 – 63,7 – 226,8 = -80,5 W/m2.
In the atmosphere: 45,5 + 335,5 + 17 + 148,3 – 318 – 27,2 – 160 = 41,1 W/ m2.
At the surface (sea): 100,7 + 318 – 375 – 17 – 148,3 = -121,6 W/ m2.
It seems that over the Aegean Sea there is negative energy budget during the winter season. That is, the solar radiation energy that enters the atmosphere until the surface (sea) is a less than the emitted Earth's radiation energy that escapes to the space by 80,5 W/m2.
However, the atmosphere holds a positive energy budget (41,1 W/m2) during winter. That means that the atmosphere over the Aegean Sea is being warmed! The positive budget in the atmosphere during the winter season is perhaps the explanation of the phenomenon where coastal areas have mild winters. Because as we see from Figure 3, the latent heat emitted from the sea (from the evaporation of sea water) is a big flux – larger from all the rest seasons!-, and equals to 148,3 W/m2 . In addition, there is also the sensible heat (winds) that seem to absorb heat from the sea transfering it to the atmosphere during the winter season with an intensity of 17 W/m2 .
What I understand is that the excess of heat the sea had absorbed during the summer is released during the winter season at a rate of 148,3 W/m2. This is carried out mainly through the evaporation of sea water (latent heat). During this process (evaporation) for every gram of sea water that evaporates about 585 calories of heat energy are taken from the sea and are released to the atmosphere above.
Note: I didn't know but I learned that the sea behaves differently from the land considering evaporation. Thus, over the Mediterranean Sea evaporation is more intense during winter (yes winter) in comparison with the rest of the seasons, while there is another period of intense evaporation during July.
In Figure 4 the energy budget of the Aegean Sea during the spring season is presented.
Figure 4. Energy budget of the Aegean Sea during spring season. Values of energy fluxes are written in W/m2.
Top of the atmosphere: 410,1 – 100 – 250,1 = 60 W/m2.
In the atmosphere: 85,8 + 339,2 + 4,4 + 67,2 – 324,8 – 20 – 170,2 = -18,4 W/m2.
At the surface (sea): 224,2 + 324,8 – 399,1 – 4,4 – 67,2 = 78,3 W/m2.
It seems that during the spring there is a positive energy budget over the Aegean Sea. That is, the solar radiation energy that enters the atmosphere until the surface (sea) is larger than the emitted Earth's radiation energy that escapes to the space by 60 W/m2.
I also observe that the evaporation of sea water has as a result the transfer of heat from the sea's body to the atmosphere by 67,2 W/m2 . This is less compared to the winter season (148,3 W/m2). Nevertheless, I read that during the spring there is minimum evaporation of sea water at the Mediterranean sea.
One reason for having surplus in the energy budget over the Aegean Sea during the spring is that the sun insolation is more intense during this time period. Also during the spring there are fewer cloudy days (which means bigger percentage of solar radiation reaches the atmosphere and the surface). At the same time period the surface (sea) is still relatively cold and so is the air above the sea. Thus the emission of infrared radiation from the sea surface (known as blackbody radiation or longwave radiation or Stefan-Boltzmann emissivity formula) is relatively low. I was surprised that May was the month of the largest net positive budget of energy of all the months , even from the summer months! This made me understand better how plants distinguish the season changes: since the plants depend on external sources of heat to get warmed, they should strongly feel the difference of transition from winter to spring or from spring to summer, etc.
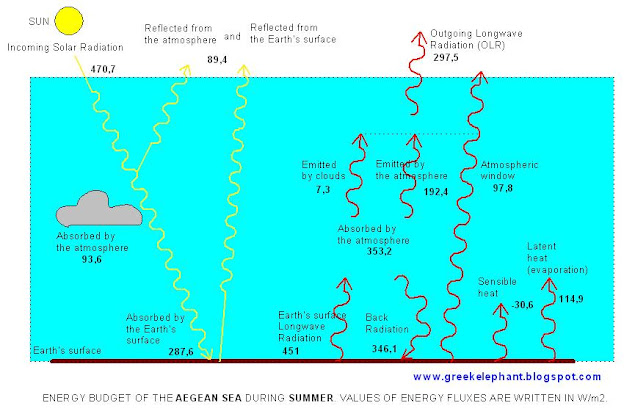
In Figure 5 the energy budget over the Aegean Sea during the summer season is presented.
Figure 5. Energy budget of the Aegean Sea during the summer season. The values of energy fluxes are written in W/m2.
Top of the atmosphere: 470,7 – 89,4 – 297,5 = 83,8 W/m2.
In the atmosphere: 93,6 + 353,2 + (-30,6) + 114,9 – 346,1 – 7,3 – 192,4 =
= –14,7 W/m2.
At the surface (sea): 287,6 + 346,1 – 451 – (-30,6) – 114,9 = 98,4 W/m2.
It seems that during the summer there is a positive energy budget over the Aegean Sea. That is, the solar radiation energy that enters the atmosphere until the surface (sea) is larger than the emitted Earth's radiation energy that escapes to the space by 83,8 W/m2.
I observe that the sensible heat (from convection of heat through the winds) is negative (-30,6 W/m2). This means that the air above the sea is warmer and thus heat from the air is being absorbed from the sea because the latter is cooler.
The heat up of the sea during the summer season is reasonable because the sun's insolation is very intense and also because there are fewer clouds in the atmosphere that reflect solar radiation to the space. However, the heat up of the sea during the summer period is not much larger than the heat up during the spring (energy budget at the surface 98,4 W/m2 during summer and 78,3 W/m2 during spring). Maybe this is due to the larger evaporation rate during the summer season (114,9 W/m2 during summer and 67,2 W/m2 during spring). It has already been referred that the evaporation of water takes large amount of heat from the sea and releases it to the air above. Also, there are other factors that determine the heat up of the sea, such as the emissivity of longwave radiation from the sea surface (blackbody radiation), the sensible heat and the back radiation (infrared/ longwave radiation from the atmosphere that is emitted back to the surface).
In Figure 6 the energy budget over the Aegean Sea during the autumn season is presented.
Figure 6. Energy budget of the Aegean Sea during the autumn season. The values of energy fluxes are written in W/m2.
Top of the atmosphere: 284,4 – 65,8 – 261,8 = -43,2 W/m2.
In the atmosphere: 59,4 + 354,8 + (-1,7) + 138,9 – 340,6 – 20,8 – 178,2 =
= 11,8 W/m2.
At the surface (sea): 159,2 + 340,6 – 417,6 – (-1,7) – 138,9 = -55 W/m2.
It seems that during the autumn there is a negative energy budget over the Aegean Sea. That is, the solar radiation energy that enters the atmosphere until the surface (sea) is less than the emitted Earth's radiation energy that escapes to the space by 43,2 W/m2.
What I understand is that during autumn the sea begins to cool down, releasing large amounts of heat to the atmosphere (energy budget at the surface -55 W/m2), mainly through the evaporation. It should be noted here that, the evaporation rate during autumn is larger then the evaporation rate during summer (138,9 W/m2 and 114,9 W/m2 correspondingly).
The sensible heat is marginally negative (-1,7 W/m2) during autumn. This means that the air temperature is a little higher than the temperature of the sea. Thus the sea absorbs heat (marginally, very little) from the winds.
The energy budget of energy in the atmosphere is positive during autumn (11,8 W/m2). That is, the atmosphere is heated up. This is due mainly to the evaporation of sea water (138,9 W/m2). Perhaps that is why coastal areas have mild temperatures during the autumn season.
Bibliography (sources)
The main sources that where used for the estimation of individual energy fluxes are the following:
1) Kiehl, J.T. and Trenberth, K.E., 1997, "Earth's annual global mean energy budget", Bulletin of the American Meteorological Society, Vol. 78, No2, p. 197-206.
2) http://www.helapco.gr/ims/file/installers/totee-klimatika.pdf
Technical Chumber of Greece, 2010, «Climatic data of areas of Greece», Ministry of Environment, Energy and Climate Change, 1st Edition, Athens.
3) http://cimss.ssec.wisc.edu/wxwise/homerbe.html
The Earth’s Radiation Energy Balance (Results from Nasa’s Earth Radiation Budget Experiment – ERBE).
4) http://onlinelibrary.wiley.com/doi/10.1029/2004JC002566/full
C. Matsoukas, A. C. Banks, N. Hatzianastassiou, K. G. Pavlakis, D. Hatzidimitriou, E. Drakakis, P. W. Stackhouse and I. Vardavas, 2005, “Seasonal heat budget of the Mediterranean Sea”, Journal of Geophysical Research: Oceans (1978-1912), Vol. 110, Issue C12, American Geophysical Union, Wiley online library.
5) http://science-edu.larc.nasa.gov/energy_budget/pdf/ERB-poster-combined-update-3.2014.pdf
National Aeronautics & Space Administration (NASA), 2009 (presented on the internet in 2014), “Earth’s Energy Budget”.
Annex (methodology)
I studied bibliography [1] adjusting the data to bibliography [5]. I created some formulas to calculate (when there where no other climatological or satellite data),
a) the absorption of solar radiation from the atmosphere and the clouds,
b) the reflection of solar radiation from the atmosphere, the clouds, the aerozol and the Earth's surface.
c) the absorption of solar radiation from the Earth's surface.
d) the «atmospheric window» (infrared/ longwave radiation of specific wavelength range which is emitted from the Earth's surface directly to the space).
e) the «Back Radiation» which is the infrared/ longwave radiation which is re-emitted from the atmosphere and the clouds back to the Earth's surface.
f) the radiation of infrared/ longwave radiation from the atmosphere to the space.
g) the absorption and re-emission of infrared/ longwave radiation from the clouds (Longwave Cloud Forcing, LWCF).
h) the ΟLR (Outgoing Longwave Radiation), that is the total infrared/ longwave radiation (of the Earth's surface and the atmosphere) that escapes to the space.
The climatic data that where used came from meteorological stations in a) Heraklion, Crete, b) Rhode Island, c) Naxos island and d) Lesvos island.
In particular from bibliography [1] I used the following data:
Average monthly temperature of the air.
From bibliography [3] I used the data of albedo (reflectivity of solar radiation) over the aegean Sea.
From bibliography [4] I used the data:
a) for the influx and outflux of heat energy from the sea (-ΔΗ) in Figure 8.
b) for the evaporation of sea water (Εr) in Figure 18.